미분 개념을 처음 접했을 때 가장 많이 보는 공식이 두가지 있다. 첫번째는 미분계수 공식이고, 두번째는 다항함수의 미분 식이다.
엄밀히, 다항함수라 하면 차수가 다른 항이 여러개로 이루어져 있는 함수이지만 단항을 먼저 증명해야 다항함수 증명까지 진행가능하므로 먼저 단항 증명을 하였다.
오늘은 미분계수와 이항정리를 이용해서 증명해보았다.
1. 미분계수
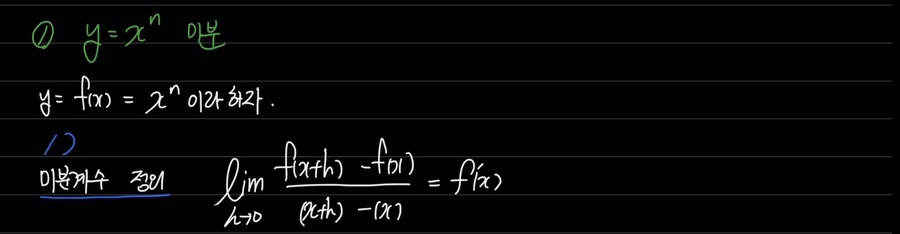
2. 이항정리

혹시 이항 정리를 모르는 분들을 위해 간단히 설명해두었다. (a,b)로 이루어진 n개의 상자에서 a와 b를 각각 뽑는다는 관점에서 접근을 했고, 조합의 기본 개념은 알고 있다고 가정했다. 사실 이 증명에서 이항 정리가 쓰이는 것은, 첫번째 항과 두번째 항을 이용하기 위함이다.
3. 두 개념 적용

가장 먼저 미분계수 개념으로 시작했고, 이항 정리 식을 사용하여 (x+h)^n의 첫번째 항은 x^n과 만나 소거가 된다. 이후 h로 나눠주게 되면 (x+h)^n의 두번째 항인 n*x^(n-1)만 남고 나머지는 0으로 수렴하게 된다.
따라서 다음과 같이 결론 지을 수 있다.

- 소고기를 사랑하는 수학자 드림 -
'지식활용소 > 수학적 지식' 카테고리의 다른 글
| 삼각함수 미분의 증명(코사인, 사인, 탄젠트) (0) | 2021.11.27 |
|---|---|
| 정적분의 증명 (a ~ b 구간 적분) (0) | 2021.11.27 |
| 시그마 K 제곱(^2)의 증명 (0) | 2021.11.27 |


